이번에 포스팅할 알고리즘은 벨먼-포드 알고리즘으로 그래프의 최단 경로를 찾는 알고리즘이다.
이 알고리즘의 이름은 개발자인 리차드 E. 벨먼[Richard E. Bellman]과 레스터 포드 주니어[Lester Ford Junior]의 이름에서 유래 한다. 벨먼은 알고리즘의 중요 분야 중 하나인 동적계획법을 고안한 사람이기도 하다.
벨먼-포드 알고리즘을 보기전에 그래프 자료구조에 대해 잘 모른다면 아래의 포스팅을 보고 오면 좋다.
[자료구조] 그래프 (Graph)
그래프라고 하면 원 그래프나 막대 그래프, 혹은 수학의 y=f(x) 그래프가 생각날 수 있다.하지만 컴퓨터 과학에서 사용하는 그래프는 좀 다르다. 이번 포스팅에서는 컴퓨터 과학에서 말하는 그래
twd0622.tistory.com
현재 차근차근 해보자는 생각에 기초 공부를 하는 중이다. 좀 더 자세한 내용은 다른 글에 작성하거나 추후 글을 수정하는 방향으로 작성해 보겠다.
틀린 내용이 있거나 궁금한게 있다면 편하게 댓글 남겨주시면 감사하겠습니다!
📝 개념
벨먼-포드 알고리즘은 그래프의 최단 경로를 찾는 알고리즘이다. 최단 경로 문제는 시작점과 끝점이 지정되어 있고, 간선에 비용이 부여된 가중 그래프가 주어졌을때, 시작점과 끝점까지의 경로 중 비용의 합이 가장 작은 것을 찾는 문제다.
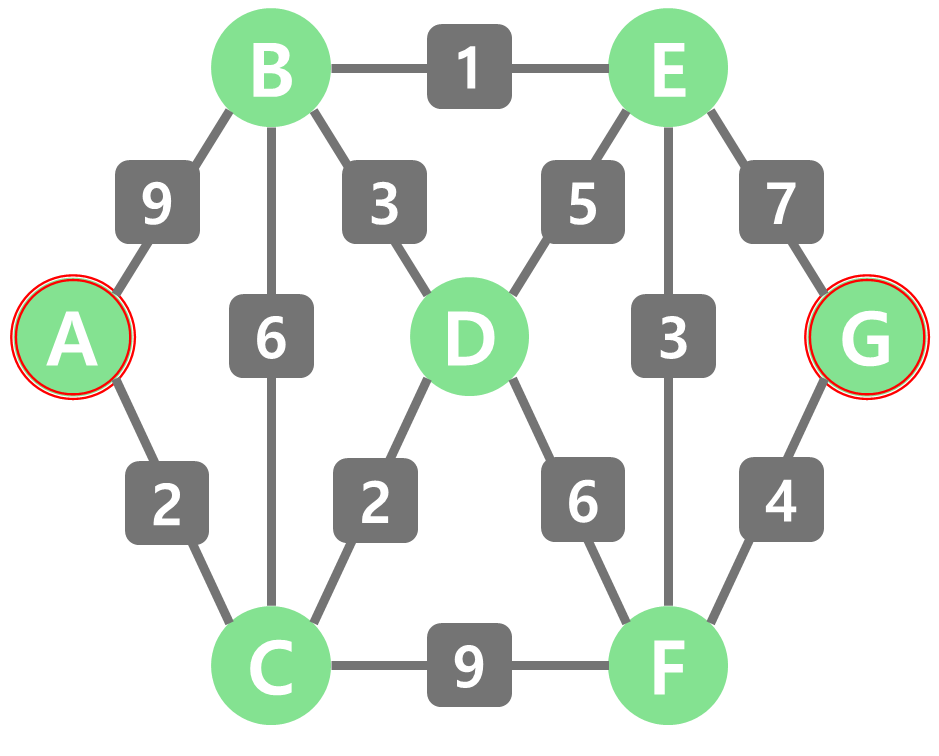
A를 시작점, G를 끝점으로 놓고 벨먼-포드 알고리즘을 설명하겠다.
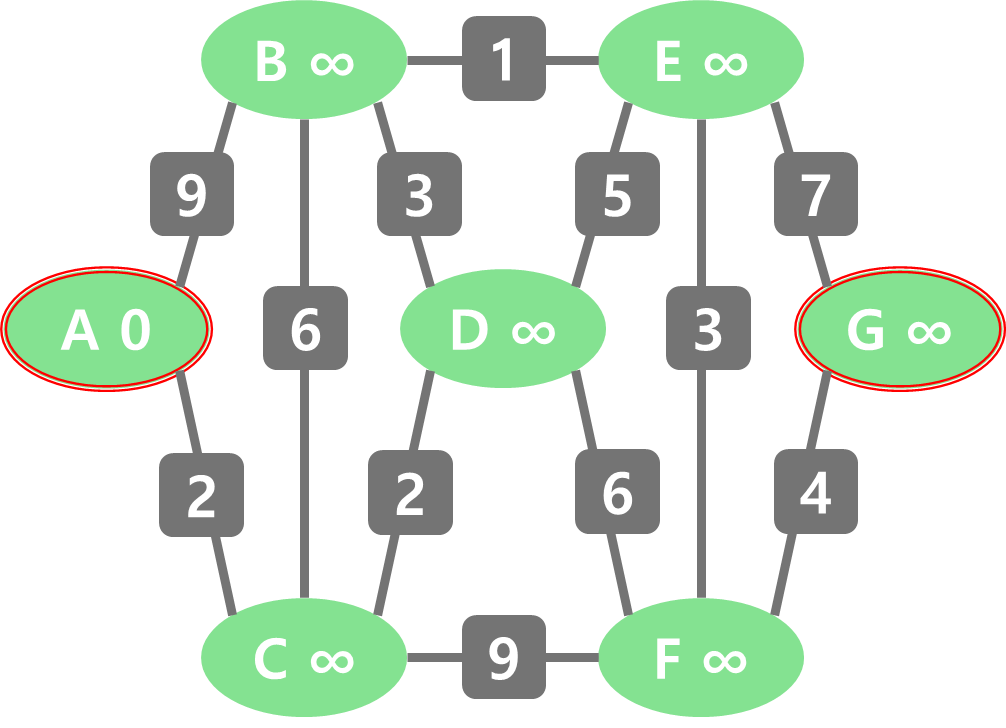
각 정점에 대해 초기 비용을 설정한다. 시작점은 0, 그 외의 정점은 무한대(∞)로 설정한다. 이 비용은 A부터 해당 정점에 이르는 최단 경로의 잠정적 길이를 의미한다. 계산이 진행됨에 따라 이 값이 점점 작아지면서 최종적으로 올바른 값에 수렴하게 된다.

간선 중에서 하나를 선택한다. A와 B를 연결하는 간선을 선택해 보겠다. 선택한 간선의 한 정점에서 다른 정점에 도달하기 위한 비용을 각각 계산한다. 계산 방법은 '출발하는 정점의 비용 + 간선의 비용' 이다. 계산은 한 방향씩 순서대로 진행하며 어느 방향 부터 계산해도 무방하다. 여기선 비용이 작은 정점에서 큰 정점으로 향하는 방향을 먼저 계산하겠다.
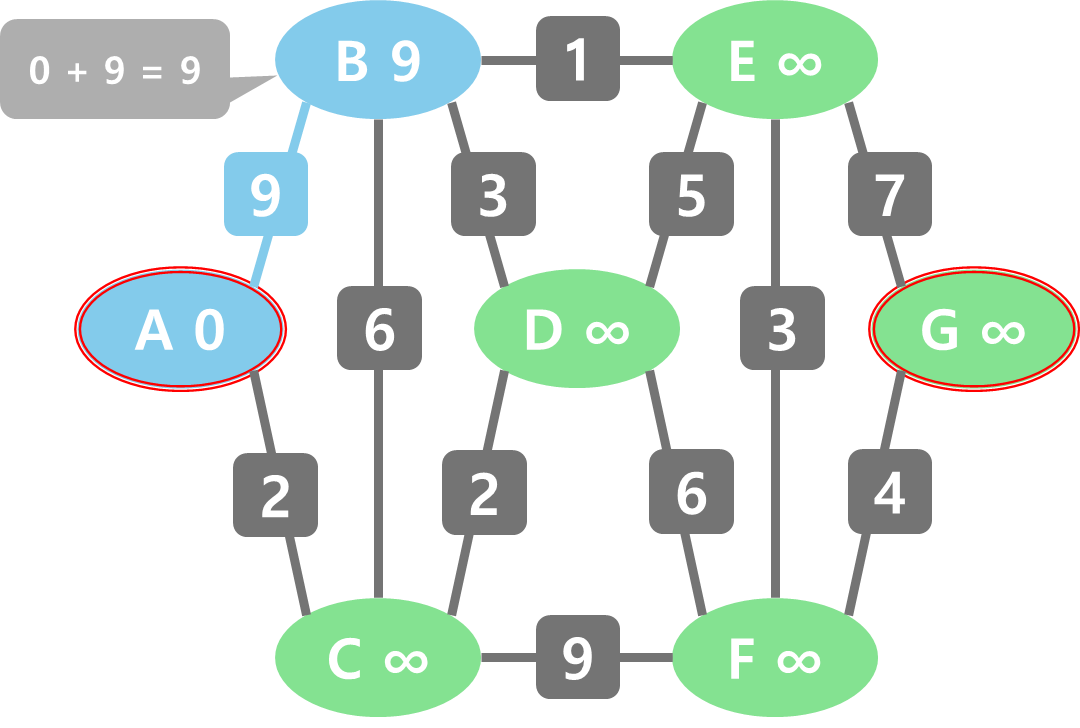
현재 정점 A가 정점 B보다 비용이 작기 때문에( 0 < ∞ ) 정점 A에서 B로 향하는 비용을 먼저 계산한다. 정점 A의 비용은 0이고 간선(A, B)의 비용은 9이므로, 정점 A에서 정점 B로 이동하는 비용은 0+9이다.

계산한 결과가 현재 값보다 작으면 정점의 비용을 새로운 값으로 갱신한다. 정점 B의 현재 값은 무한대이고 9가 더 작기 때문에 비용을 9로 갱신했다. 값이 갱신된 경우 어떤 정점에서 시작된 경로인지 기록해 준다. 여기선 살구색(?)으로 기록해 두겠다.

이어서 역방향으로 정점 B에서 정점 A로 이동하는 경우를 계산한다. 정점 B의 비용은 9이므로, 정점 B에서 정점 A로 이동하는 비용은 9 + 9 = 18이다. 정점 A의 현재 값인 0과 비교하면 현재값이 더 작기 때문에 정점의 비용은 갱신되지 않는다.
비용이 큰 정점에서 작은 정점으로 향하는 경우 간선의 비용이 음수가 아닌 이상 갱신되지 않는다.

모든 간선에 대해 동일한 처리를 수행한다. 처리할 간선의 순서는 임의로 정해도 무방하지만, 여기선 왼쪽에 있는 간선부터 계산하겠다. A에서 C로 가는 간선을 선택을 하겠다.
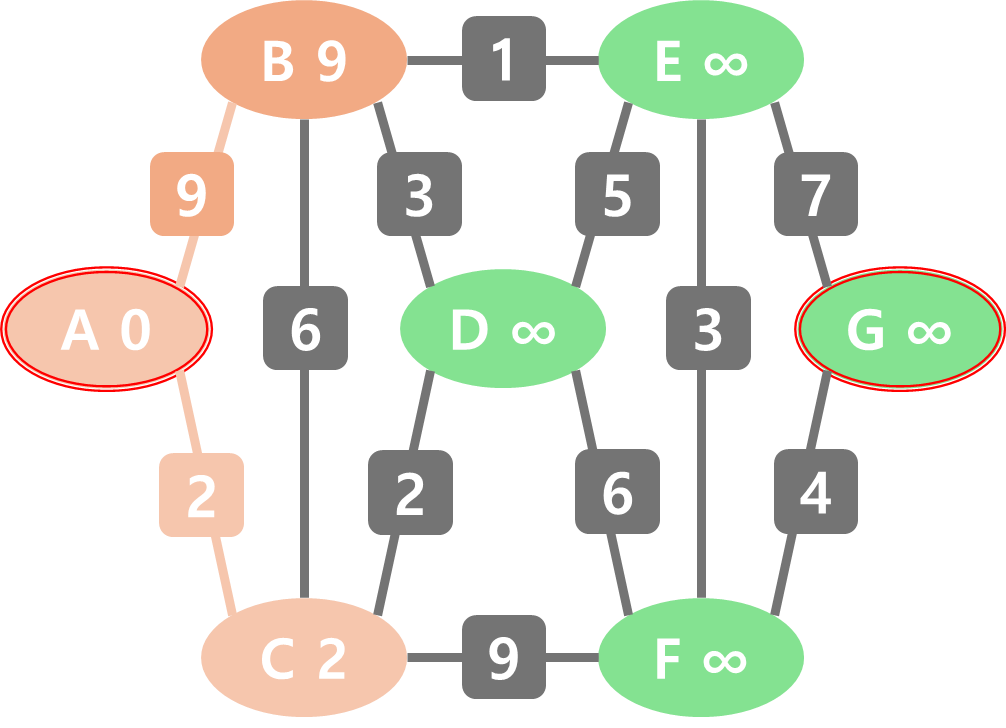
A의 정점 0과 간선(A, C)의 비용 2를 더하면 0 + 2 = 2 이다. 때문에 C의 비용을 2로 갱신해준다.

동일하게 간선을 하나 더 선택하고..

정점 C의 비용 2와 간선(C, B)의 비용 6을 더하면 2 + 6 = 8이기 때문에 원래 비용인 9보다 더 적은 비용이 나온다. 그래서 B의 비용은 8로 갱신이 된다.
현시점에서는 정점 A에서 B로 가는 경우, 곧바로 가는 것보다 정점 C를 경유하는 것이 비용이 더 적음을 알 수 있다.

이제 모든 간선에 대하여 갱신 작업을 빠르게 진행 하겠다.

간선(B, D)는 8 + 3 = 11 로 D의 비용 11, 간선(B, E)는 8 + 1 = 9로 E의 비용 9 가 된다.

간선(C, D)는 2 + 2 = 4로 D는 4로 갱신이 되고, 간선(C, F)는 2 + 9 = 11로 F의 비용은 11이 된다.

이런 식으로 나머지 간선들도 모두 한차례 계산을하면 위의 그림처럼 된다. 이제 지금까지 했던 작업을 비용이 변경되지 않을 때 까지 반복해서 진행한다.

2번째 갱신 작업을 했다. 정점 B의 비용이 8에서 7로, 정점 E의 비용이 9에서 8로 변경 되었기 때문에 갱신 작업을 한번 더 수행한다.

3번째 갱신 작업이 완료되었다. 정점의 비용이 더 이상 변경되지 않았으므로 작업을 완료한다. 이 시점에서 알고리즘의 탐색이 완료되며 시작점에서 모든 정저메 대한 최단 경로가 도출되었다.

지금까지의 탐색으로 시작점 A에서 도착점 G에 대한 최단 경로는 빨간색으로 표시한 A-C-D-F-G이며 비용은 14가 된다.
여기 까지가 벨먼-포드 알고리즘 탐색 방법이였다.
✔️ 추가 내용
최단 경로 문제에서 간선의 비용은 시간이나 거리, 요금을 나타내기 때문에 양수인 것이 일반적이다. 하지만 벨먼-포드 알고리즘은 간선의 비용이 음수인 경우에도 정상적으로 동작한다.
그러나 간선 비용의 합이 음수가 되는 폐로가 있는 경우에는 그 폐로가 비용 갱신 작업을 순회하면 계속해서 경로의 비용을 줄일 수 있을 것이다. 즉, 애당초 최단 경로가 존재하지 않는다는 뜻이다. 이때 정점의 비용 갱신 작업을 N회 반복해도 정점의 비용이 계속 변경 되므로 '최단 경로가 존재하지 않는다'라고 판단할 수 있다.
⏱️ 시간복잡도
주어진 그래프의 정점 수를 n, 간선 수를 m이라 하고 계산 시간을 알아보겠다.
벨먼-포드 알고리즘은 비용 갱신 작업을 n차례 수행하면 완료된다. 한 차례에 걸리는 시간은 O(m)이다. 따라서 전체 계산 시간은 O(nm)이 된다.
참고 자료
그림으로 이해하는 알고리즘 : 이시다 모리테루, 미야자키 슈이츠
'코딩 테스트 > 알고리즘' 카테고리의 다른 글
| [알고리즘] A* (에이 스타) 알고리즘 (1) | 2025.02.07 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (Dijkstra Algorithm) (1) | 2025.02.06 |
| [알고리즘] 깊이 우선 탐색 (DFS, Depth-First Search) (4) | 2025.01.17 |
| [알고리즘] 너비 우선 탐색 (BFS, Breadth-First Search) (0) | 2025.01.17 |
| [알고리즘] 병합 정렬 (Merge Sort) (3) | 2024.10.16 |



