현재 차근차근 해보자는 생각에 기초적인 부분을 공부하고 있다. 좀 더 구체적인 내용은 다른 글에 작성하거나 추후 글을 수정하는 방향으로 해보겠다.
틀린 내용이 있거나 궁금한게 있다면 편하게 댓글 남겨주시면 감사하겠습니다.
📌 개념
퀵 정렬은 기준이 되는 수(피봇(pivot)이라고 함)를 수열 안에서 임의로 하나 선택한다. 그리고 피봇 이외의 수를 '피봇보다 작은 수'와 '피봇보다 큰 수'의 두 그룹으로 나누고, 이것을 다음과 같이 배치한다.
[피봇보다 작은 수] < 피봇 < [피봇보다 큰수]
이제 각 [ ] 안을 정렬하면 전체가 정렬된다. [ ] 안을 정렬할 때도 다시 퀵정렬을 사용한다.

임의의 수열로 퀵정렬을 실시해 보겠다.
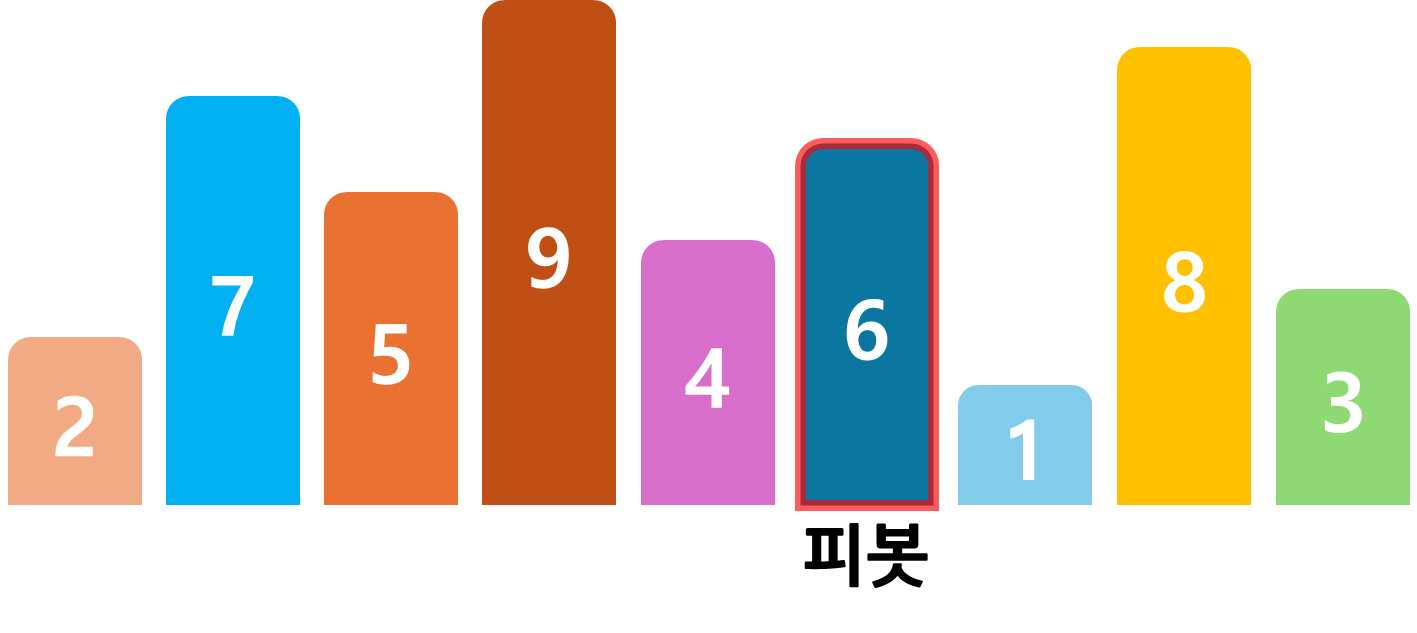
기준이 되는 수(피봇)을 임의로 하나 선택한다. 여기서는 6을 선택해 보겠다.
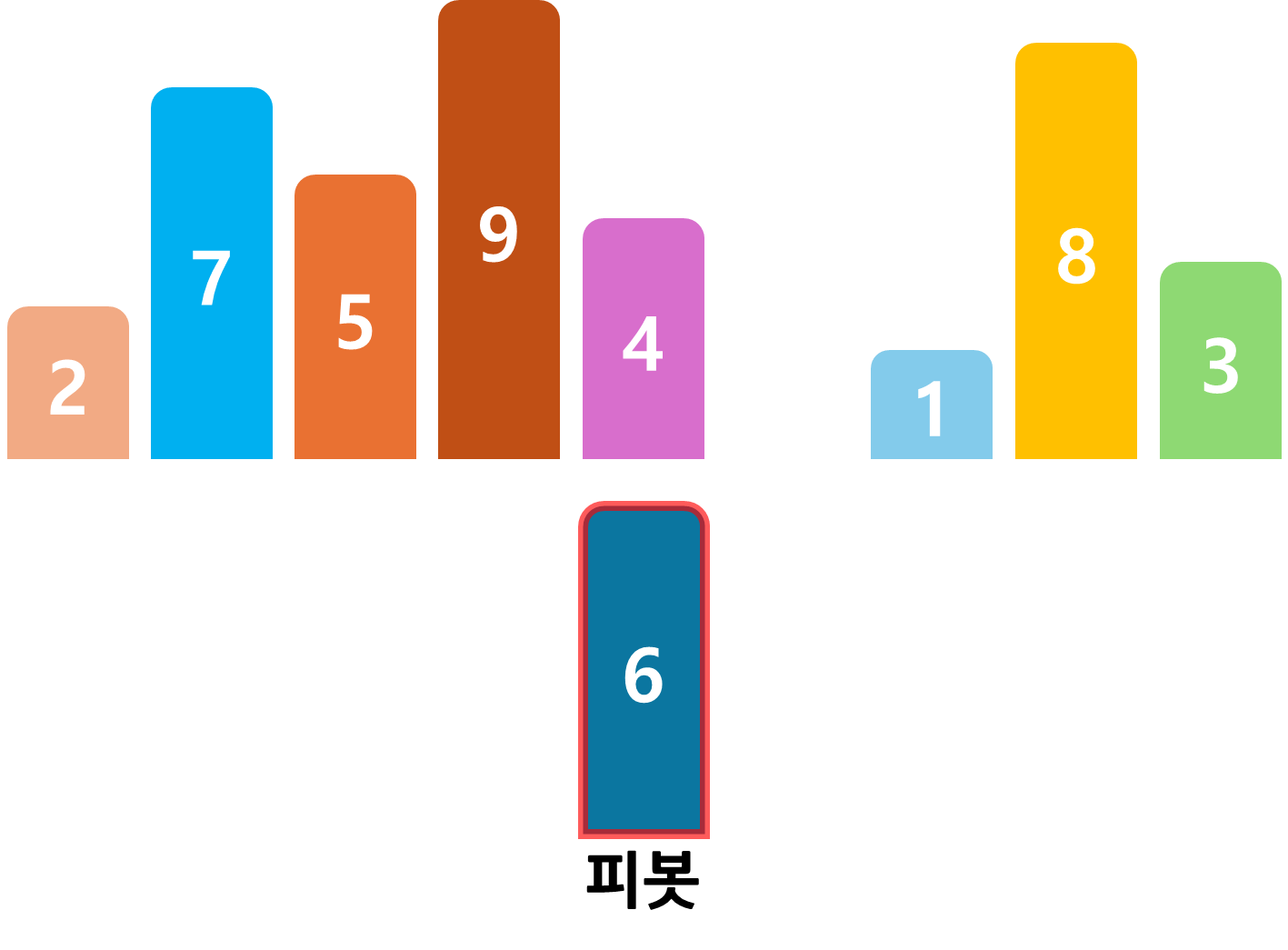
피봇 이외의 각 숫자를 피봇과 비교한다. 피봇보다 작은 숫자는 왼쪽, 큰 숫자는 오른쪽으로 이동한다.

가장 앞의 숫자 2는 피봇인 6과 비교하면 2 < 6 임으로 피봇 왼쪽으로 간다.

다음 숫자 7은 피봇과 비교하면 7 > 6 이기 때문에 피봇의 오른쪽으로 이동한다.

이런 식으로 수열을 차례대로 정렬하면 위와 같은 결과를 얻는다.
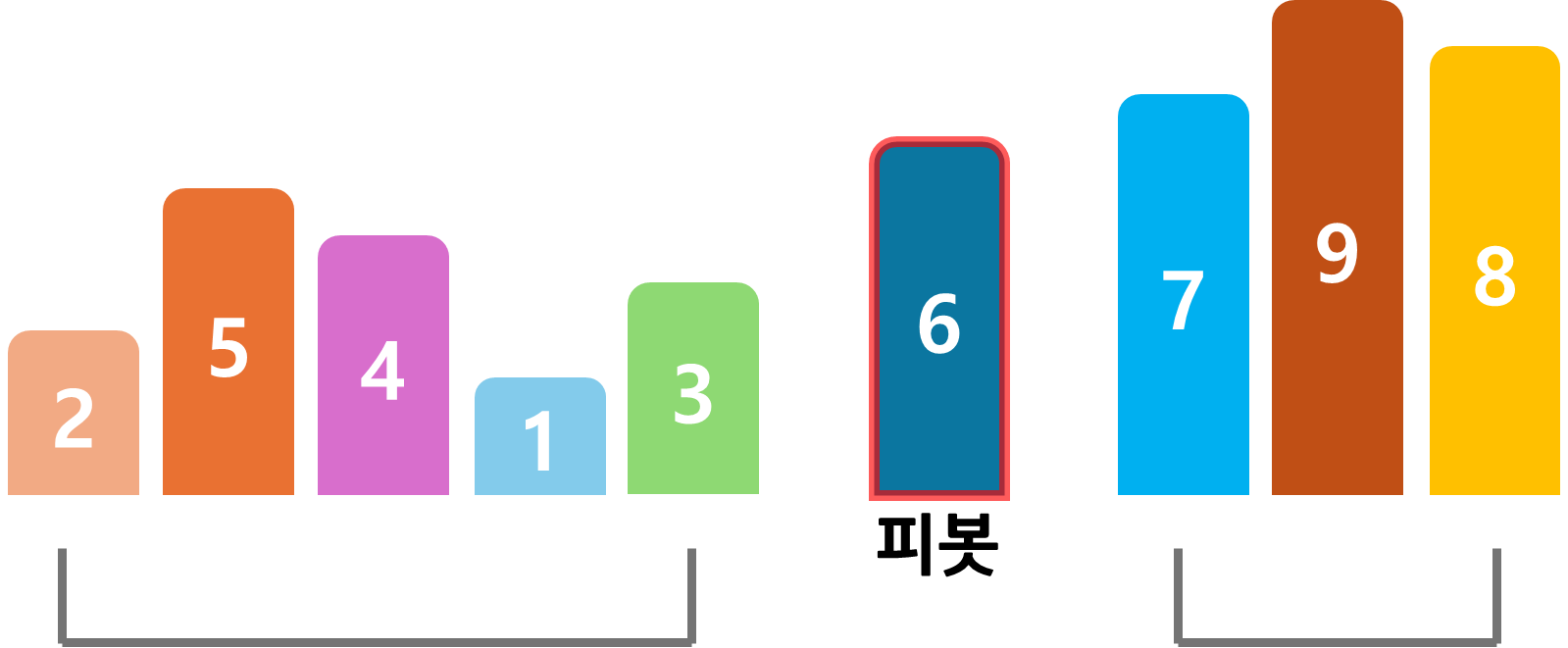
이제 피봇의 왼쪽에는 작은 수들이 오른쪽에는 큰 수들이 있어 각각 정렬하면 전체 정렬이 완료된다.

우선 왼쪽 작은 수들의 수열부터 다시 퀵 정렬을 해보겠다.
피봇은 임의로 4로 잡고 정렬을 하면

위 결과를 얻을 수 있다.
오른쪽 큰 수는 5 하나 뿐이라 정렬이 완료되었고, 왼쪽 남은 수들을 또 다시 퀵정렬 해준다.

피봇을 2로 잡고 퀵정렬을 실시하면

위 결과가 만들어 진다.

이렇게 최초의 피봇인 6 기준으로 왼쪽의 수열들이 정렬이 완료되었다.

이제 오른쪽 수열을 퀵정렬 해준다.
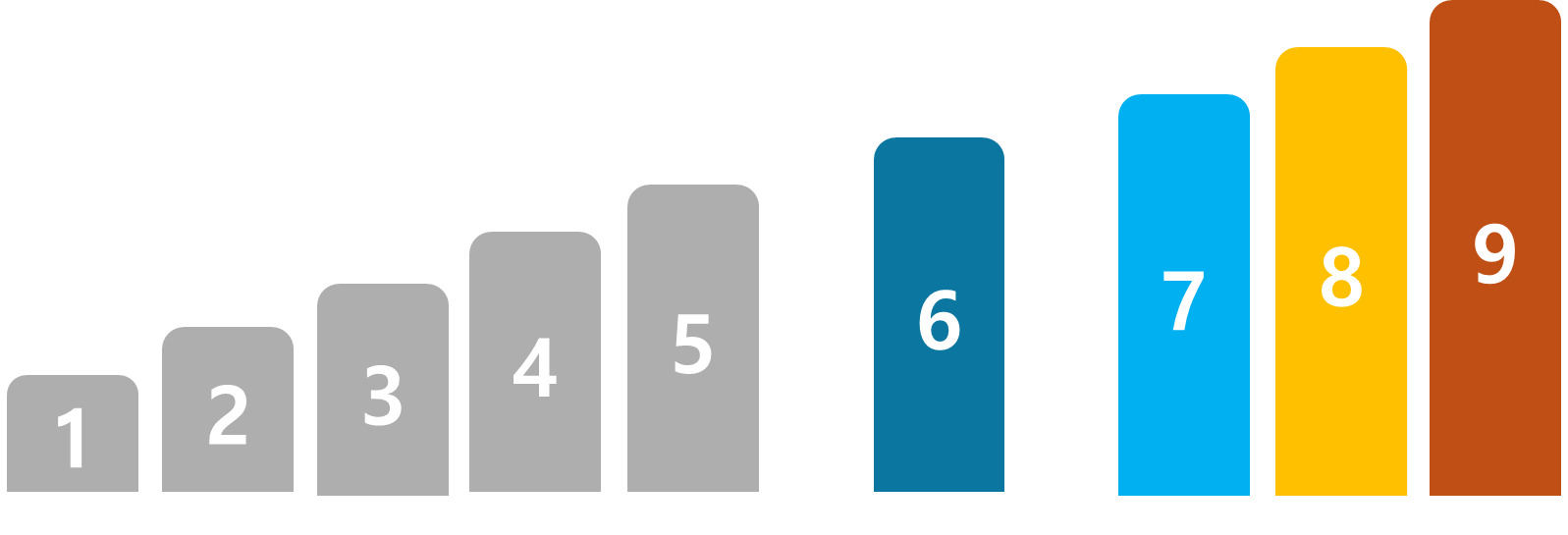
같은 방법으로 정렬을 해주면 이렇게 1부터 9까지의 숫자가 정렬된것을 확인 할 수 있다.
📌 추가 내용
퀵 정렬은 분할정복법(divide-and-conquer)에 해당한다. 원래 문제를 두 자식 문제(피봇보다 작은 것과 큰 것)로 분할하고, 두 자식 문제를 해결하는 것을 반복하면 원하는 결과를 얻을 수 있다.
자식 문제를 해결하기 위해 퀵정렬을 다시 사용하는 것 처럼 알고리즘 내부에서 알고리즘 자신을 사용하는 것을 재귀라고 한다. (해당 내용은 추후에 정리하겠다.)
퀵정렬은 속도가 빠르다는 점과 추가 메모리 공간을 필요로 하지 않는다는 점이 장점이다.
시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
또한 퀵정렬은 O(log n)만큼의 메모리를 필요로 한다.
단점은 정렬된 리스트에 대해서는 퀵정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다는 점이다.
그리고 퀵 정렬에서 피벗을 선택할 때 불균형 분할을 방지하기 위하여 리스트를 균등하게 분할할 수 있는 데이터가 선택되도록 해야한다.
⏱️ 시간복잡도
자식 문제를 만들기 위해 피봇을 선택할 때 두 자식 문제를 원래 문제의 반이 되도록 매번 피봇을 선택면 퀵 정렬의 계산 시간은 병합 정렬과 마찬가지로 O(n log n)이다. 이는 병합 정렬의 경우와 마찬가지로 자식 문제의 크기를 절반으로 만드는 과정을 log₂n회 반복하면 숫자 하나로 구성된 자식 문제가 되어 정렬된 상태가 되기 때문이다.
그리고 분할 될때 마다 숫자들은 피봇과 한번씩 비교하므로 계산 시간은 O(n)이다.
따라서 전체 계산 시간은 O(n log n)이다.
참고 자료
그림으로 이해하는 알고리즘 : 이시다 모리테루, 미야자키 슈이츠
[알고리즘] 퀵 정렬(quick sort)이란 : Heee's Development Blog https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 병합 정렬 (Merge Sort) (3) | 2024.10.16 |
|---|---|
| [알고리즘] 힙 정렬 (Heap Sort) (0) | 2024.09.09 |
| [알고리즘] 이진 탐색 (Binary Search) (0) | 2024.09.04 |
| [알고리즘] 삽입 정렬 (Insertion Sort) (0) | 2024.08.21 |
| [알고리즘] 선택 정렬 (Selection Sort) (0) | 2024.08.13 |



